Hero for Book Review: Algorithms to live by
· Book Review · 10 min read

Book Review: Algorithms to live by

Takeaway

An algorithm is a defined process to follow to get a desired result. Much of our lives are decided by algorithms. Knowing what algorithms to follow can result in more efficient and effective decision making.

Algorithms in life

I recently re-read Algorithms to Live By, a book by Brian Christian and Tom Griffiths on how algorithms can help us be more effective in our lives. Having picked up programming last year, I got more out of this time around.

An algorithm is a process, and you can think of it as instructions to follow to complete some task. For example, learning how to add numbers together is a simple algorithm 1.

More complex instructions can calculate results for other problems in life. Interest rates, web search rankings, or social media feeds are all based on the output of algorithms. The book goes through many such algorithms, and relates them to problems you might face personally.

It’s too difficult to explain every algorithm they mention 2, so instead I’ll be doing short highlights from some, and usually concentrating on the qualitative, not quantitative takeaways.

Also, most of the algorithms rely on certain assumptions; rather than specify that every time, take that as a given when reading. I’ll add some of the assumptions in footnotes for those interested.

Some of the problems discussed include:

  • When to stop interviewing for the max chance of the best outcome
  • When you should stop exploring new options to enjoy the ones you already know
  • How to schedule your tasks based on what your goal is

Let’s look at our first algorithm, on when you should stop working on a problem.

Optimal stopping

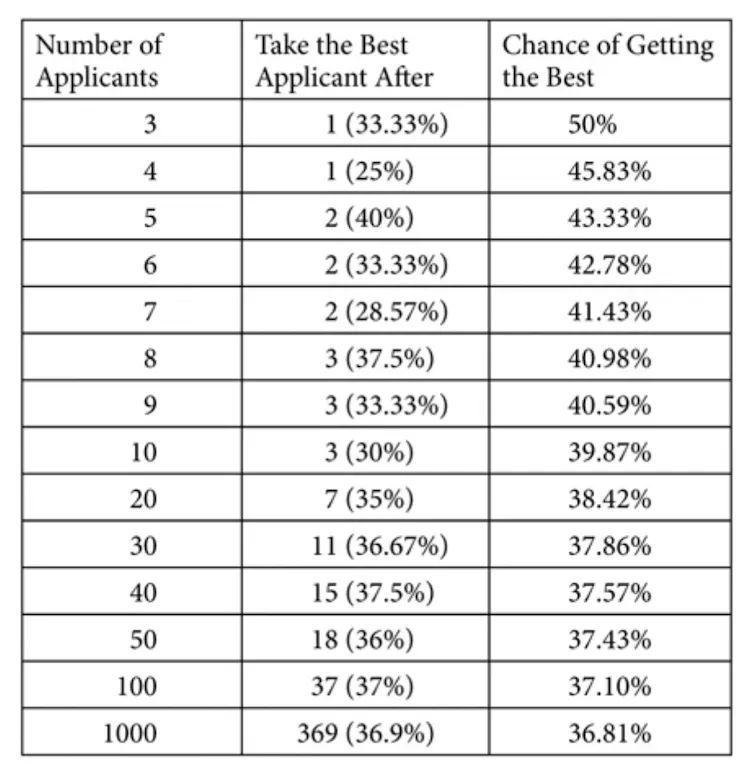
If you’re evaluating options (job applicants, housing offers, parking spaces etc), there’s a tradeoff between how long you spend choosing, and the chance of picking the “best” option. This is known as the secretary problem - suppose you were hiring a secretary, how many interviews should you do to get the best chance of finding the best one?

In this case, there’s a precise percentage to use. You should wait after seeing 37% of the applicant pool, and then take the next best applicant you see 3. For example, if you had 100 applicants, wait after you’ve seen the first 37, and then pick the next applicant that is better than all you’ve seen so far.

That is the mathematically optimal point with the highest chance of picking the best person for the job. If you stop too early, you might miss someone interviewing later. If you stop too late, you waste time 4.

post

Explore exploit

Similar to the optimal stopping situation, there’s a tradeoff between information gathering (explore) and enjoying (exploit). Suppose you’re at a casino, and want to decide which machines to play. You want to maximise your winnings, but don’t know the exact odds for the machines (if you did, you’d play the best one).

In this case, there’s a number, known as the Gittins Index, that gives you the optimal machine to play 5. If you know the number of wins, losses, and how much you value future gains, you can calculate precise values for each choice. Some interesting properties:

  • If you’re playing the optimal machine and win again, it makes sense to continue playing that machine
  • If you’re playing the optimal machine and lose once, it might still make sense to continue playing that machine
  • An entirely unknown machine can be preferable to machines that are known to win often, and that unknown machine gets more valuable the more you value future gains

Some other related implications:

  • Exploration has a higher impact younger in life; babies putting everything in their mouth makes sense from their standpoint
  • Exploiting has a higher impact later in life; hence older people cutting down their social network and preferring to return to favourite restaurants

Sorting

The book gave a few examples of sorting algorithms, which are commonly used in programming. For example, returning search results requires a sorting of the most relevant ones for you.

I’ll save more detailed discussion of sorting algos for another day since they require understanding time complexity. Here are some qualitative takeaways:

  • Some ways of sorting can be drastically more efficient than others (>10x faster)
  • Some scenarios do not desire sort efficiency only. For example, arranging a sports season matchup calendar also requires taking into account how exciting the season will be. You could optimise sort efficiency, but the season will seem less thrilling
  • The more efficient a sort, the more fragile it might be against accidental mistakes. For example, the “best” team might accidentally get knocked out in a single elimination tournament (essentially a sorting algo) like the World Cup 6.

Caching and memory

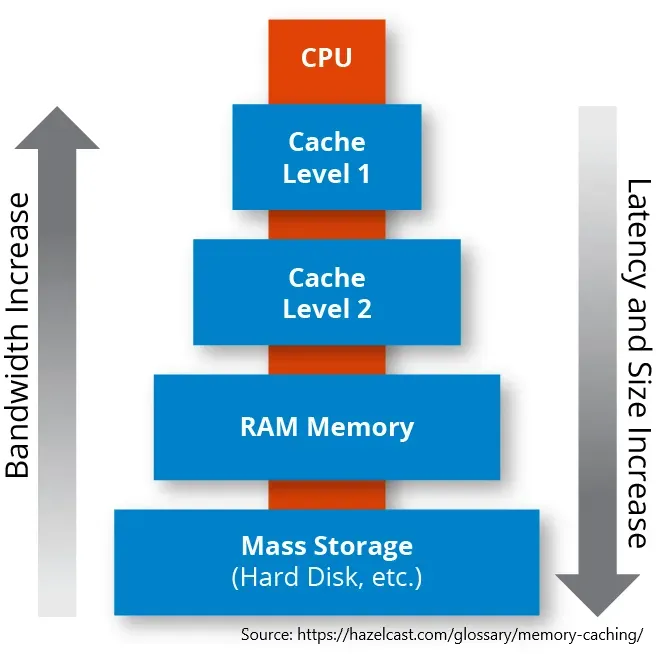
The idea of having a cache is to have 1) a small, fast memory (storage) section, and 2) a large, slow memory section. We’ll then alternate between the two depending on what our intention is. This lets us get both some amount of speed and some amount of size for the activity we want.

For example, you might have your favourite clothes in your wardrobe, and your unused ones in the attic. You’d have quick access to the items you used the most, but still have space for that ugly christmas sweater if you wanted. Caching sounds complicated, but you’ll realised we do it naturally for most of our daily lives.

How do you decide what items should be put in the fast section, and what items in the slow section? You could put random items, the newest item, the largest item etc.

In this case, keeping the most recently used items in the small and fast section is the optimal choice, due to something known as temporal locality. You’re more likely to need something again that’s something you’ve recently used. For example, google drive highlights your frequently used files for quick access.

post

Scheduling

Most of us have to decide how to prioritise items on our to do list. This usually requires making a tradeoff between responsiveness (how quickly you respond) and throughput (how much you can get done).

A key point about scheduling and prioritisation is defining your goal metric, since that determines what algorithm you want to use 7. Maximising responsiveness comes at the expense of how much you can get done:

If you want to minimise the max lateness of all your projects 8, the Earliest Due Date algorithm tells you to start with the project due earliest.

If you want to minimise the total completion time, the Shortest Processing Time algorithm tells you to just do the quickest task first.

If your tasks are not equal in importance, then placing a weight on each task and calculating the weight over time required ratio will help you decide which task to do; pick the project with highest weight over time.

Practically, this means that it’s probably worth having a conversation with your manager on how the team thinks about this tradeoff, and which method they’d prefer you adopt.

There’s another important concept in scheduling, which is the idea of context switching - whenever you have to switch between tasks. Context switching is wasted time since it’s not real work, but takes up time and effort on your part.

For example, if you were writing an email and then got interrupted by a slack message, it takes time for you to both respond to the slack message, and then remember what you wanted to do for the email.

At its worst, context switching turns to thrash, when you get nothing productive done because you’re too busy with only switching. Ways to avoid thrash include:

  • Saying no to tasks, though the authors acknowledge we’re often unable to do so
  • Working dumber and more inefficiently. Rather than think about the optimal way to get through your tasks, just start on something and get it done

Bayes rule and distributions

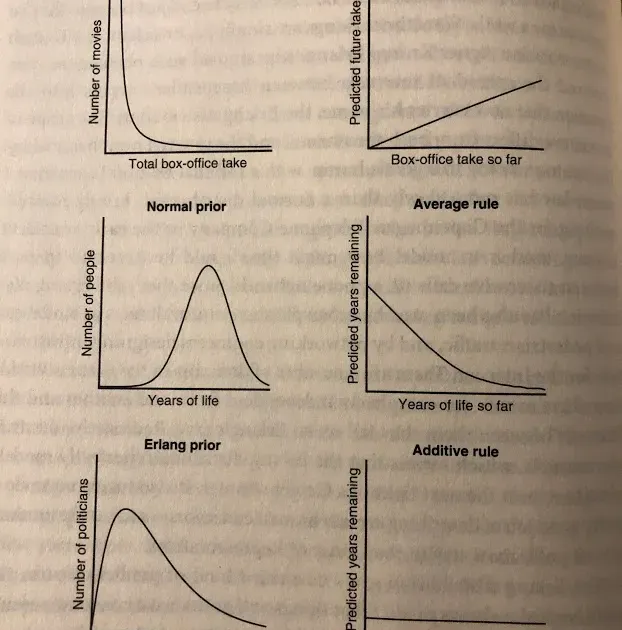
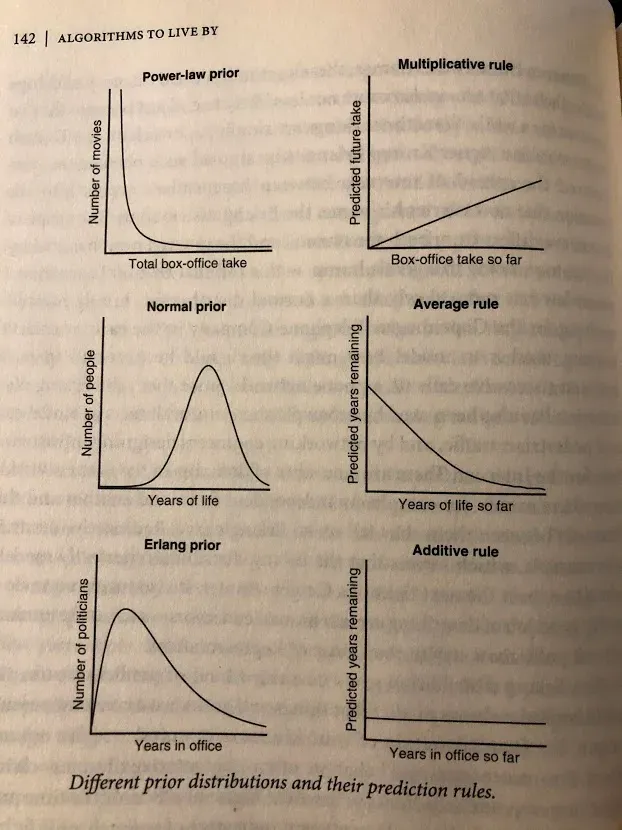
Explaining Bayes rule would probably take an article on its own, so let’s just take it as a rule that helps you with predicting how likely something is to occur 9. What the authors want to highlight is that this depends on the distribution that your events are coming from. There are three main distributions to think about:

  • Power law: the longer something has gone on, the longer we expect it to continue going on. For example, if a company has been growing a long time, we’d expect it to continue growing
  • Normal: early events are surprising, late events are expected. For example, we’d be surprised by people who die early in life, and not by people who die late in life.
  • Erlang: events are never any more or less surprising. For example, a memoryless distribution of a roulette wheel or the coin flips we discussed last week

post

Game theory

Most of us have probably heard of game theory before, which is a way of thinking what the optimal strategy is when playing a game. Some highlights:

  • If you play too many levels above your opponent, you’re going to think they have information they don’t actually have, and they won’t be able to think what you want them to think. Put another way, you don’t want to get too smart with your strategies
  • Every two player game has at least one Nash Equilibrium, where both players are choosing the optimal strategy for themselves
  • However, finding Nash equilibrium is an intractable problem, meaning there’s limits to the practicality of game theory
  • The equilibrium may also not be the outcome that is best for all players. It may be optimal for an individual to compete, but optimal for the group to cooperate. We can quantify this as the “price of anarchy”, which measures the gap between cooperation and competition.
  • There’s also a counterintuitive concept known as mechanism design, which shows that worsening every outcome might actually make everyone better off, due to shifting the equilibrium

Besides the algorithms mentioned above, the authors also go through:

  • When you might be overfitting your decision making process and what you can do about it
  • What to do when real world problems aren’t as nice as theory and why you should relax constraints
  • How to think about information networking and how the internet works

Overall I thought the book was worth reading to get an overview of interesting ways algorithms show up in life. I did understand it better after learning some computer science though, so keep that in mind. I also wish that they’d included more practical examples 10, since trying to apply the findings to life can be difficult when you have to work off different assumptions.

Footnotes

  1. Easy enough to teach children, by telling them to memorise sums and when to carry a number, but surprisingly not obvious when trying to implement on a computer, see full adder logic gate ↩

  2. You might say that by the time I explain everything, I might as well have written the entire book ↩

  3. The percentage is 1 divided by e, euler’s number. The chance doesn’t change as the size of the applicant pool grows, but does change with different information states you get ↩

  4. The base secretary problem assumes that you can’t go back to a candidate that you passed on, but there are variations that resemble real life a bit more closely. ↩

  5. This problem is intractable if the probabilities of a payoff on a machine change over time; essentially meaning it’s unsolvable. Some problems are intractable. In these cases, relaxing some constraints and accepting solutions that are “close enough” helps us significantly in structuring the problem. ↩

  6. Or March Madness, for the Americans ↩

  7. Only 9% of all scheduling problems can be solved efficiently. ↩

  8. As in, take all your projects that are late, and then the maximum of those. That’s the metric you want to minimise. ↩

  9. See here for an article that explains Bayes. Bayes is unintuitive (for me at least), which also means its good to know ↩

  10. To be fair, there’s a good amount of information in the footnotes elaborating more ↩

Related Posts

Comments